Giải Toán Hình 12 Nâng Cao Chi Tiết, Đầy Đủ, Sách Giáo Khoa Hình Học 12 Nâng Cao

Lớp 1

Tài liệu Giáo viên

Lớp 2

Lớp 2 - liên kết tri thức

Lớp 2 - Chân trời sáng tạo

Lớp 2 - Cánh diều

Tài liệu Giáo viên

Lớp 3

Lớp 3 - kết nối tri thức

Lớp 3 - Chân trời sáng sủa tạo

Lớp 3 - Cánh diều

Tài liệu Giáo viên

Tài liệu Giáo viên

Lớp 4

Lớp 4 - kết nối tri thức

Lớp 4 - Chân trời sáng tạo

Lớp 4 - Cánh diều

Tiếng Anh lớp 4

Tài liệu Giáo viên

Lớp 5

Sách giáo khoa

Sách/Vở bài xích tập

Tài liệu Giáo viên

Lớp 6

Lớp 6 - liên kết tri thức

Lớp 6 - Chân trời sáng sủa tạo

Lớp 6 - Cánh diều

Tiếng Anh

Tài liệu Giáo viên

Lớp 7

Lớp 7 - liên kết tri thức

Lớp 7 - Chân trời sáng sủa tạo

Lớp 7 - Cánh diều

Tiếng Anh

Tài liệu Giáo viên

Lớp 8

Lớp 8 - kết nối tri thức

Lớp 8 - Chân trời sáng sủa tạo

Lớp 8 - Cánh diều

Tiếng Anh

Tài liệu Giáo viên

Lớp 9

Sách giáo khoa

Sách/Vở bài xích tập

Tài liệu Giáo viên

Lớp 10

Lớp 10 - liên kết tri thức

Lớp 10 - Chân trời sáng sủa tạo

Lớp 10 - Cánh diều

Tiếng Anh

Tài liệu Giáo viên

Lớp 11

Lớp 11 - kết nối tri thức

Lớp 11 - Chân trời sáng sủa tạo

Lớp 11 - Cánh diều

Tiếng Anh

Tài liệu Giáo viên

Lớp 12

Sách giáo khoa

Sách/Vở bài xích tập

Tài liệu Giáo viên

thầy giáo

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Để học tốt Toán lớp 12 nâng cao, loạt bài giải bài tập Toán 12 cải thiện được biên soạn bám đít theo văn bản sách giáo khoa Giải Tích 12 cải thiện và Hình học tập 12 nâng cao.

Bạn đang xem: Giải toán hình 12 nâng cao

Giải bài tập SGK Toán 12 nâng cao

Giải tích 12 nâng cao

Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ vật dụng thị của hàm số

Chương 2: Hàm số lũy thừa, hàm số mũ và hàm số lôgarit

Chương 3: Nguyên hàm, tích phân và ứng dụng

Chương 4: Số phức

Hình học 12 nâng cao

Chương 1: Khối đa diện với thể tích của chúng

Chương 2: phương diện cầu, mặt trụ, khía cạnh nón

Chương 3: cách thức tọa độ trong không gian

23 bài bác giảng Toán lớp 12 - Thầy trần gian Mạnh (Giáo viên Viet
Jack)

36 videos các dạng bài bác tập Toán lớp 12 - Cô Nguyễn Phương Anh (Giáo viên Viet
Jack)

Tài liệu triết lý và các dạng bài tập Toán lớp 12:

CHỈ TỪ 250K 1 BỘ TÀI LIỆU GIÁO ÁN, ĐỀ THI, KHÓA HỌC BẤT KÌ, VIETJACK HỖ TRỢ DỊCH COVID

Bộ giáo án, đề thi, bài bác giảng powerpoint, khóa học giành cho các thầy cô và học viên lớp 12, đẩy đủ các bộ sách cánh diều, kết nối tri thức, chân trời sáng tạo tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo Viet
Jack Official

- Chọn bài bác -Bài 1: Hệ tọa độ trong ko gianBài 2: Phương trình khía cạnh phẳng
Bài 3: Phương trình đường thẳng
Ôn tập chương 3Ôn tập cuối năm
Một số đề kiểm tra

Xem cục bộ tài liệu Lớp 12: trên đây

Sách giải toán 12 một số đề kiểm tra (Nâng Cao) giúp đỡ bạn giải những bài tập vào sách giáo khoa toán, học giỏi toán 12 sẽ giúp đỡ bạn rèn luyện khả năng suy luận phải chăng và hợp logic, hình thành khả năng vận dụng kết thức toán học vào đời sống cùng vào những môn học tập khác:

Đề hàng đầu (trang 129 sgk Hình học tập 12 nâng cao):

Câu 1: cho hình chóp tứ giác rất nhiều S.ABCD gồm đáy bằng a, và ở bên cạnh bằng a√2.

a) Tính thể tích của hình chóp vẫn cho.Bạn đang xem: Giải toán hình 12 nâng cao

b) Tính bán kính mặt mong ngoại tiếp hình chóp S.ABCD.

c) call A’ và C theo lần lượt là trung điểm của hai cạnh SA với Sc. Minh chứng rằng hình chóp A’.ABCD cùng C’CBAD bởi nhau.

Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(4; -1; 2); B(1; 2; 2), C(1; -1; 5)

a) minh chứng rằng ABC là tam giác đều.

b) Viết Phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ.

c) Viết phương trình trục của mặt đường tròn ngoại tiếp ΔABC

d) search tọa độ điểm D sao cho ABCD là tứ diện đều.

Lời giải:

Câu 1:

a) điện thoại tư vấn H là trung ương của hình vuông ABCD

Ta có SH ⊥ (ABCD)

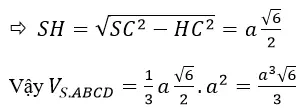
b) call O là giao điểm của SH và và mặt đường trung trực cạnh SA, suy ra O là tâm mặt cầu ngoại tiếp S.ABCD.

Ta có: SO.SH=SA’.SA (A’ là trung điểm SA)

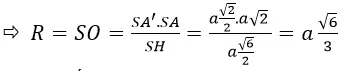
c) Ta thấy nhì hình chóp A’.ABCD cùng C’.ABCD đối xứng với nhau qua mp(SBD) buộc phải chúng bởi nhau. (đpcm)

Câu 2:

a) Ta tất cả AB = AC = BC = 3√2 buộc phải tam giác ABC là tam giác đều.

b) Mp(ABC) là phương diện phẳng đia qua A(4; -1; 2) cùng nhận =(9;9;9) làm cho vectơ pháp tuyến đường nên tất cả phương trình là: x+y+z-5=0

Mặt phẳng (ABC) cắt trục tọa độ lần lượt tại:

M(5; 0; 0); N(0; 5; 0), P(0; 0; 5)

Thể tích khối chóp OMNP là:

c) Trục của đường tròn nước ngoài tiếp tam giác ABC là đường trải qua tâm đường tròn nước ngoài tiếp ΔABC với vuông góc cùng với mp(ABC). Trung khu đường tròn ngoại tiếp là điểm M thõa mãn MA = MB = MC

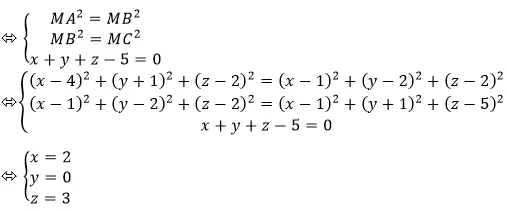
Vậy trục của đường tròn là đường thẳng đi qua M(2; 0; 3) và nhận vectơ =(9;9;9) làm cho vectơ chỉ phương nên gồm Phương trình là:

d) Để ABCD là tứ diện đông đảo thì D nằm trên trục đường tròn nước ngoài tiếp ΔABC cùng DA = AB = 3√2

Vì D vị trí trục mặt đường tròn ngoại tiếp ΔABC phải tọa độ của D gồm dạng: D(2+t; t; 3+t).

Vì domain authority = 3√2 DA2=18 (2-t)2+(1+t)2+(1+t)2=18

3t2=12 => t2=4 => t=±2

Với t = 2 => D(4; 2; 5); cùng với t = -2=> D(0; -2; 1)

Vậy có hai điểm D vừa lòng bài toán.

Đề số 2 (trang 129 sgk Hình học 12 nâng cao):

Câu 1: mang đến tứ diện hầu như ABCD cạnh bởi a. Gọi B’, C’, D’ theo lần lượt là trung điểm những cạnh AB, AC, AD.

a) minh chứng rằng 6 điểm B, C, D, B’, C’, D’ nằm trên một khía cạnh cầu.

b) Tính thể tích khối chóp D.BCC’B’

Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(2; 0; 0); A’(6; 0; 0), B(0; 3; 0); B’(0; 4; 0); C(0; 0; 4); C’(0; 0; 3).

a) Viết phương trình khía cạnh cầu trải qua 4 bốn điểm A, A’, B, C. Minh chứng rằng: B’ và C’ cùng nằm bên trên mặt ước đó.

Xem thêm: Nghệ Tươi Ngâm Mật Ong Để Được Bao Lâu, Mật Ong Để Được Bao Lâu

b) minh chứng rằng trực chổ chính giữa H của tam giác ABC, trọng tâm G của ΔA’B’C’ thuộc nằm trên một mặt đường thẳng trải qua O. Viết Phương trình đường thẳng đó.

c) Tính khoảng cách từ điểm O cho tới giao điểm của mp(ABC’) cùng (A’B’C)

Lời giải:

Câu 1:

Gọi H là trung khu của ΔBCD, khi đó AH ⊥ (BCD) với AH là trục con đường tròn nước ngoài tiếp ΔB’C’D’

a) hotline M là trung điểm BB’ với O là giao điểm của con đường thẳng AH với con đường trung trực OM của cạnh BB’.

Khi đó ta có:

=> O cách đều 6 điểm B, C, D, B’, C’, D’ hay O là tâm mặt cầu đi qau B, C, D, B’, C’, D’. Bán kính mặt mong là R = OB.

Ta có:

Mặt không giống tam giác vuông AMO đồng dạng tam giác vuông AHB

c) Tính V(D.BCC.B.). Khoảng cách từ D đến mo(ABC) cũng bằng đoạn AH (vì tứ diện ABCD đều).

Diện tích hình thang cân nặng B’C’CB là

Vậy thể tích khối chóp D.BCC’B’ là:

Câu 2:

a) điện thoại tư vấn Phương trình phương diện cầu trải qua A, A’, B, C là:

x2+y2+z2+ax+by+cz+d=0

Vì mặt ước đi qau A(2; 0; 0); A’(6; 0; 0); B(0; 3; 0), C(0; 0; 4) cần ta bao gồm hệ:

Vậy Phương trình mặt cầu là: x2+y2+z2-8x-7y-7z+12=0

Thay tọa độ điểm B’ và C cùng phương trình mặt ước thấy thõa mãn. (đpcm)

b) Trực vai trung phong H của ΔABC là

Trọng trung khu G của ΔA’B’C’ là

Suy ra phương trình mặt đường thẳng HG là:

Đề số 3 (trang 130 sgk Hình học 12 nâng cao):

Câu 1: mang đến hình vỏ hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB, vị (α) là mặt phẳng trải qua 3 tư điểm D, N, B’.

a) Mp(α) cắt hình vỏ hộp đã mang đến thiếu diện là hình gì?

b) chứng tỏ rằng phương diện phẳng (α) phần phân chia khối hộp đã mang lại thành nhì khối đa diện H1 với H2 bởi nhau.

c) Tính tỉ số thể tích của khối đa diện H1 cùng thể tích tứ diện AA’BD.

Câu 2: Trong không khí tọa độ Oxyz cho những điểm: A(1; -3; -1); cùng B(-2; 1; 3)

a) minh chứng rằng nhì điểm A với B giải pháp đều trục Ox.

b) search điểm C vị trí Oz làm sao để cho tam giác ABC vuông trên C.

c) Viết phương trình hình chiếu của mặt đường thẳng AB bên trên mp(Oyz).

d) Viết phương trình mặt cầu đi qua ba điểm O, A, B và tất cả tâm nằm trên mp(oyz).

Lời giải:

Câu 1:

a) do số khía cạnh phẳng cắt mặt phẳng song song theo nhị giao tuyến song song phải α cắt hình vỏ hộp theo tiết diện là hình bình hành DNB’N’.

b) H1 và H2 là nhì hình đa diện đối xứng cùng nhau qua trung khu O của hình hộp phải chúng bằng nhau.

c) vị H1 với H2 bằng nhau nên thể tích của chúng bằng một thể tích hình hộp.

Mặt khác

Câu 2:

a) Ta có: d(A,Ox)=d(B,Ox)=√10 (đpcm)

Vì ΔABC vuông trên C bắt buộc CA2+CB2=AB2

1+9+(1+c)2+41+(3-c)2=9+16+16

2c2-4c-16=0 c = 4 và c = -2

Vậy điểm C thỏa mãn bài toàn là: C = (0; 0; 4) cùng C’(0; 0; -2)

c) Hình chiếu của A(1; -3; -1) lên mp(Oyz) là A’(0; -3; -1)

Hình chiếu của B(-2; 1; 3) lên mp(Oyz) là B’(0; 1; 2)

Vậy A’B’ chính là hình chiếu của AB lên mp(Oyz). Phương trình con đường thẳng A’B’ là:

Lớp 1

Đề thi lớp 1

Lớp 2

Lớp 2 - liên kết tri thức

Lớp 2 - Chân trời sáng sủa tạo

Lớp 2 - Cánh diều

Tài liệu tham khảo

Lớp 3

Lớp 3 - kết nối tri thức

Lớp 3 - Chân trời sáng tạo

Lớp 3 - Cánh diều

Tài liệu tham khảo

Lớp 4

Sách giáo khoa

Sách/Vở bài bác tập

Đề thi

Lớp 5

Sách giáo khoa

Sách/Vở bài bác tập

Đề thi

Lớp 6

Lớp 6 - liên kết tri thức

Lớp 6 - Chân trời sáng sủa tạo

Lớp 6 - Cánh diều

Sách/Vở bài xích tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 7

Lớp 7 - liên kết tri thức

Lớp 7 - Chân trời sáng tạo

Lớp 7 - Cánh diều

Sách/Vở bài bác tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 8

Sách giáo khoa

Sách/Vở bài bác tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 9

Sách giáo khoa

Sách/Vở bài bác tập

Đề thi

Chuyên đề và Trắc nghiệm

Lớp 10

Lớp 10 - liên kết tri thức

Lớp 10 - Chân trời sáng sủa tạo

Lớp 10 - Cánh diều

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 11

Sách giáo khoa

Sách/Vở bài bác tập

Đề thi

Chuyên đề & Trắc nghiệm

Lớp 12

Sách giáo khoa

Sách/Vở bài tập

Đề thi

Chuyên đề & Trắc nghiệm

IT

Ngữ pháp tiếng Anh

Lập trình Java

Phát triển web

Lập trình C, C++, Python

Cơ sở dữ liệu

Giải bài xích tập Toán 12 nâng cao
Giải tích 12 nâng cao Hình học tập 12 nâng cấp Toán lớp 12 nâng cao | Giải bài bác tập SGK Toán 12 nâng cấp chi tiết, đầy đủ

Toán lớp 12 nâng cao | Giải bài xích tập SGK Toán 12 nâng cấp chi tiết, đầy đủ

Để học giỏi Toán lớp 12 nâng cao, loạt bài giải bài xích tập Toán 12 cải thiện được biên soạn bám sát đít theo nội dung sách giáo khoa Giải Tích 12 cải thiện và Hình học 12 nâng cao.

Giải tích 12 nâng cao

Chương 1: Ứng dụng đạo hàm để điều tra khảo sát và vẽ thiết bị thị của hàm số

Chương 2: Hàm số lũy thừa, hàm số mũ cùng hàm số lôgarit

Chương 3: Nguyên hàm, tích phân cùng ứng dụng

Chương 4: Số phức

Hình học tập 12 nâng cao

Chương 1: Khối nhiều diện và thể tích của chúng

Chương 2: phương diện cầu, phương diện trụ, khía cạnh nón

Chương 3: phương pháp tọa độ trong ko gian

23 bài giảng Toán lớp 12 - Thầy thế gian Mạnh (Giáo viên Viet
Jack)

36 videos các dạng bài bác tập Toán lớp 12 - Cô Nguyễn Phương Anh (Giáo viên Viet
Jack)

Tài liệu triết lý và các dạng bài xích tập Toán lớp 12:

Giới thiệu kênh Youtube Viet
Jack

Ngân mặt hàng trắc nghiệm miễn tầm giá ôn thi THPT đất nước tại khoahoc.cisnet.edu.vn

CHỈ CÒN 250K 1 KHÓA HỌC BẤT KÌ, cisnet.edu.vn HỖ TRỢ DỊCH COVID

Tổng phù hợp các video dạy học tập từ những giáo viên tốt nhất - CHỈ TỪ 399K tại khoahoc.cisnet.edu.vn